This page includes detailed information on all of the 2021 Summer Illustrating Math workshops at the Park City Math Institute. General information about the structure of the program and workshops may be found on the home page.
Blender for mathematicians: a beginner’s workshopRémi Coulon
Blender is an open source 3D graphics software, popular among digital artists for its organic virtual sculpting environment and advanced animation tools. This workshop is intended for beginners. No prerequisite in computer graphics is needed. During the sessions, participants will learn how to use native structures (meshes, bezier curves, nurbs, etc) along with Python scripts to build and modify objects. We will also cover the use of “nodes” to control features in Blender, allowing one to interact with models by dynamically changing control parameters. Finally, participants will learn how to export their models for 3D printing, animate a simple scene, and render it with lights and textures.
Our first meeting will be held jointly with the Grasshopper Workshop, so participants can understand the differences between these computer graphics packages.
- What prerequisite knowledge or skills will the workshop assume?
Linear Algebra, Solid geometry, Parametric curves and surfaces.
A first experience with Python is a plus, but absolutely not mandatory.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
- Download and install the latest version of Blender (currently 2.93)
- Download the “Animation nodes” add-on for Blender (latest version)
A three button mouse is highly recommended (but not mandatory).
Participants are encouraged to come with ideas of objects / animations they would like to create. It can be a simple project such as reproducing an existing object you like. Practicing on concrete examples will make the office hours / peer collaboration time more efficient.
- What outcomes should participants expect to achieve by the end of the workshop?
The students will learn how to create, animate/print 3D models in Blender. To that end we will explore various techniques (direct modeling/sculpting, parametric description, node based programming, etc).
Blender is an extremely rich tool with an active community producing numerous add-ons. We have no intent to be exhaustive. The student will gain familiarity with the software so that they can explore it by their own later. - Will there be specific projects for participants, or should participants have their own projects in mind already?
Students are encouraged to come with their own project. A list of projects will also be provided.
Illustrating Mathematics with Grasshopper
Dave Bachman
Grasshopper is a visual scripting platform for Rhino 3D. David Bachman is a level 2 certified Rhino instructor and author of Grasshopper: Visual Scripting for Rhinoceros 3D. Rhino 3D is the predominant CAD tool in the field of Architecture, as it allows one to build models using precise construction tools, as well as by scripting with several programming languages. For this reason, it has also become popular among Mathematicians for creating mathematical models. Grasshopper is an auxiliary program which allows one to build objects in Rhino by an easy to use “visual” scripting language. Grasshopper code has several advantages over traditional scripting. Most notably, it allows for the ability to isolate a specific element of the model being built and dynamically interact with and modify it in a large variety of ways. Participants in this workshop will learn the basics of model building with Grasshopper. Depending on time and interest, we may also explore more advanced topics such as popular plug-ins to enhance the functionality of Grasshopper (e.g. Anemone for looping, Kangaroo for physics simulation, etc.), interfacing with external scripts, optimizing code for parallel processing, etc.
Our first meeting will be held jointly with the Blender Workshop (in Rémi Coulon’s Blender Zoom room, see the link on Sococo), so participants can understand the differences between these computer graphics packages.
- What prerequisite knowledge or skills will the workshop assume?
Linear Algebra and familiarity with Parametric Curves and Surfaces. Some knowledge of Differential Geometry may be helpful, but is not necessary.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
Download and install Rhino 7. There is a free trial version available that will work for the period of the Workshop.
- What outcomes should participants expect to achieve by the end of the workshop?
Students will learn how to build 2- and 3-dimensional models by creating flowcharts in Grasshopper. This will entail gaining familiarity with the wide variety of the available Grasshopper components, and an understanding of the way Grasshopper handles data structures and data flow. Students will also become familiar with some of the more popular plug-ins to expand Grasshopper’s functionality, such as Daniel Piker’s Kangaroo Physics package.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
It would be best if students came with their own projects, but I will have some ideas to choose from if they do not.
Traditional CAD/CAM Software for Mathematical Models
Glen Whitney
This tutorial provides an introduction to traditional CAD/CAM drawing tools, a class of software that may be unfamiliar to many in the mathematics and mathematical illustration community.
The first session will be joint with Edmund Harriss’ workshop on Mathematical CNC Toolpaths (and held in the CNC Toolpaths Zoom room), so that participants can sample both aspects of CAD/CAM in mathematical contexts and select one track or the other for subsequent sessions.
Note this workshop has a few specific preparation tasks that you should complete beforehand.
The particular perspective of creating materials for mathematical outreach will serve as this workshop’s vehicle for introducing the tools. It will comprise (at least) one 2D project and one 3D project. In particular, participants will model a modular-origami-style unit and produce cut files to allow the automatic production of interlockable units on consumer machines (such as the Silhouette Cameo or Cricut Explore). Sample cut units of their designs will be sent to all participants following the workshop.
As a 3D project, participants will develop rigid hubs that can be used with drinking straws to assemble one or two polyhedra of their choice. (For example, the acute and obtuse golden rhomboids that can tile space aperiodically make a nice target.) Time permitting, we will add features such as internal magnets to allow the resulting models to attach to one another. The resulting hub designs can be exported in formats suitable for 3D printing or even injection molding.
The workshop will use only freely-available, open-source software.
- What prerequisite knowledge or skills will the workshop assume?
There are no prerequisites beyond high-school solid geometry; in particular, no familiarity with CAD/CAM or any specific software is assumed.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
Briefly, participants need to install the required software, choose a modular origami unit to model, and choose a polyhedron or two to model hubs for (the hubs will allow the polyhedra of your choice to be assembled with drinking straws). Details on all of these items have now been posted.
- What outcomes should participants expect to achieve by the end of the workshop?
Students will become familiar with the operations and workflows available in 2D and 3D CAD/CAM programs. They will design a flat, cut analogue of a modular origami unit, several copies of which will be mailed to them. And they will design a hub for assembling drinking straws, which can be 3D printed by a variety of machines or on-line services.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
Lists of possible projects will be provided, but participants may choose their own.
Mathematical CNC Toolpaths
Edmund Harriss
CNC (Computer Numerical Control) machining has a rather high barrier to entry, but has a lot of mathematical potential. CNC provides a fantastic example in Linear Algebra (a machine comes with its own basis!), multivariate calculus, and many advanced geometry courses. In addition, as the objects created are made of wood (or brick, or metal, though that will not be covered here), they often become artworks in their own right becoming compelling paths into mathematical ideas.
Participants will get to create lines and paths and see the effects when these get cut into wood. On the first four days they will create a cut file that will be cut in the afternoon, so they can see the results the next day. On Friday there will be a virtual show of the completed work.
- What prerequisite knowledge or skills will the workshop assume?
No knowledge will be assumed, but we will be using Rhino/Grasshopper, so familiarity is a positive, and otherwise a willingness to play with new software is required.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
Install and spend a little time looking at Rhino/Grasshopper there are a good collection of learning resources here: https://www.rhino3d.com/learn/ (focus on the grasshopper tutorials). There is a 90-day free trial if you do not have institutional access.
- What outcomes should participants expect to achieve by the end of the workshop?
Students will have prepared the toolpaths for four pieces that will have been cut on a machine, so they can see the results. High quality photos will be provided and there might be options to ship the pieces if people prefer.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
The goal is to see the potential of the manufacturing system, rather than develop specific projects. Thoughts and ideas on what might be possible are encouraged, but we will be working through a curated collection of projects.
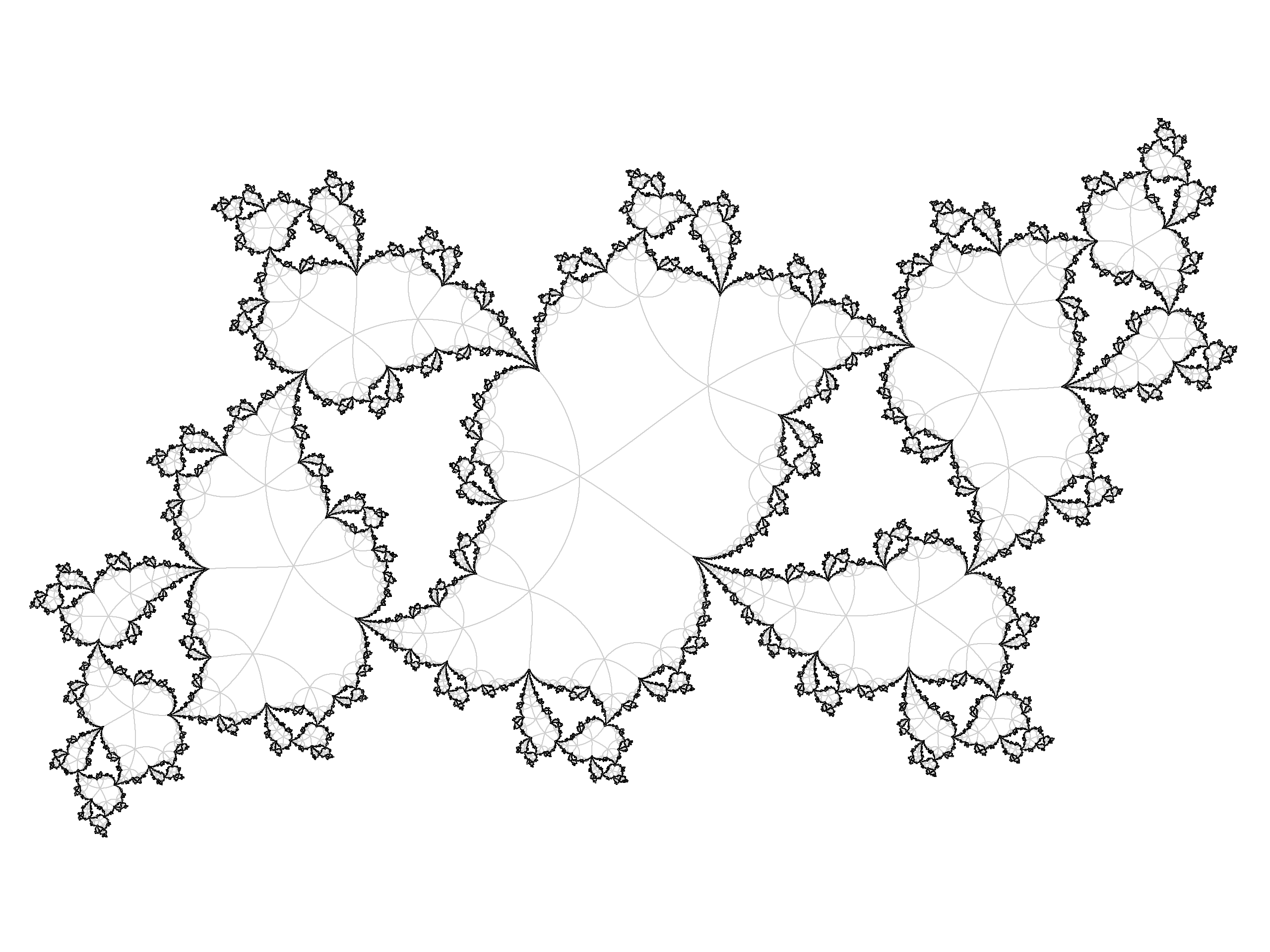Drawing Julia Sets
Arnaud Chéritat
We will review techniques for drawing Julia sets. Methods covered include classical algorithms from the 80’s and more recent ones, and a few tricks from the teacher. We will focus on quality and the workshop will include some general advice about images. Prerequisites include knowledge of complex numbers and rudiments of programming. The goal is for students to be able to draw their own Julia sets, and we have specific projects in mind.
- What prerequisite knowledge or skills will the workshop assume?
Complex numbers, basics of programming.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
In short : install GCC and libpng, compile “hello world”, know basics of (typed, procedural) programming. For details, see the bottom of the page for this workshop.
- What outcomes should participants expect to achieve by the end of the workshop?
Be able to draw their own Julia sets.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
The workshop leader will provide one (or several) specific projects.
Graphic Novels Can Teach Mathematics
Audrey Nasar
In the United States, graphic novels are increasingly being used for scholastic purposes across the curriculum as supplements or replacements for traditional textbooks. In particular, there are a number of graphic novels that explore mathematical concepts in algebra, calculus, statistics, and even graduate level mathematics. Some examples include Apostolos Doxiadis and Christos H. Papadimitriou’s Logicomix: An Epic Search for Truth, Andrew Granville and Jennifer Granville’s Prime Suspects: The Anatomy of Integers and Permutations, Larry Gonick’s Cartoon Guide to series, and The Manga Guide to series.
In this four-session minicourse [no Friday session], we will explore how graphic novels and comics can be used to teach mathematics. The sessions will begin with an introduction to the graphic medium followed by a study of several mathematically themed graphic novels, which participants will analyze according to their narrative approach, graphic style, and pedagogical content. In the sessions that follow, participants will choose mathematical concepts and then work on creating a storyline, developing characters, and drawing thumbnails for a short graphic novel (2-3 pages) to teach the concept. Participants will share and critique each others’ ideas and then revise and finalize their work.
- What prerequisite knowledge or skills will the workshop assume?
There are no prerequisites for this workshop.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
During the workshop participants will be asked to draw. This can be done using a paper and pen or pencil or using a stylus and tablet. For those drawing on paper, please make sure you have the necessary tools to quickly scan in the drawings and share them with us. Please feel free to contact me before the workshop if you would like suggestions for how to scan without a proper scanner.
Additionally, If a participant has never read a graphic novel or comic book before it may be worth picking one up and browsing through.
Examples of mathematical graphic novels to reference include Solution Squad by Jim McClain, Logicomix: An Epic Search for Truth by Apostolos Doxiadis, Prime Suspects: The Anatomy of Integers and Permutations by Andrew Granville and Jennifer Granville, Larry Gonick’s Cartoon Guide to series, and The Manga Guide to series.
- What outcomes should participants expect to achieve by the end of the workshop?
By the end of the workshop students will have created a 1-2 page comic that teaches a mathematical concept.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
Participants should choose a mathematical concept that they would like to teach in their comic. Since we will be making a short comic, I recommend starting with something simple (i.e. not the central limit theorem!).
Visualizing Mathematical Structures with Processing
Roger Antonsen
We look at how mathematical structures, in particular discrete structures and sets of finite objects, can be visualized, and interactively experimented with. Our vehicle will be Processing, an open-source, easily accessible computer programming language and environment based on Java. We start from scratch and look at how to implement and visualize structures like relations, functions, sets, equivalence classes, groups, and graphs.
- What prerequisite knowledge or skills will the workshop assume?
Anyone can attend this workshop without any prior knowledge of Processing or programming, but having some experience with programming will make things easier. In any case, we’ll spend part of the first session reviewing the basics, like variable declarations, assignments, data types, iteration, and control structures.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
No preparation is necessary. Bring good energy and a healthy curiosity!
- What outcomes should participants expect to achieve by the end of the workshop?
By the end of this workshop, the goal is that each participant will be able to take any mathematical structure or concept, and have some idea of how to visualize it and make it more tangible. Each participant should have a toolkit with a variety of tools and methods for creating mathematical visualizations.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
The workshop will be centered around broad topics, like number theory and number sequences, graph theory and simulations, cellular automata, and abstract algebra and tilings. There will be smaller projects and exercises within these topics for the participants to work on, but everyone should feel free to bring their own project to the workshop.
Interactive Videos for Teaching and Visualization
Yuri Sulyma
Participants will learn to create videos that viewers can manipulate/interact with, with a focus on mathematical content. (See liqvidjs.org and epiplexis.xyz for examples.) Topics include: using TeX in videos, 2d graphs, 3d graphics, coding demos, animation, and other forms of interactivity.
Participants are strongly advised to learn as much as they can about HTML, CSS, frontend JavaScript, React, and TypeScript (in that order) in advance of the workshop. These topics will be reviewed, and help will be available for them, but the focus will be on using the Liqvid software which is built on top of them. We also recommend coming with a concrete idea (ideally even a rough script) for a video you want to work on throughout the week. Contact yuri_sulyma@brown.edu with questions.
- What prerequisite knowledge or skills will the workshop assume?
Some familiarity with the command line and HTML.
- What specific preparation or tasks should participants have completed prior to the beginning of the workshop?
a) have a plan/script for a video they’d like to produce (here script means in the reading sense not the programming sense).
b) learn the basics of HTML, CSS, JavaScript, React, TypeScript. (Participants can contact the workshop facilitator for guidance for this.)
- What outcomes should participants expect to achieve by the end of the workshop?
Complete or mostly complete an interactive video.
- Will there be specific projects for participants, or should participants have their own projects in mind already?
They should have their own projects in mind already.